最长公共子串和最长公共子序列

自己在刷LeetCode时遇见了最长公共子串这个题目，传统的编程思想使我对此题无从下手，后面查阅资料后了解到动态规划这一思想，因此便写下文章，记录如何使用动态规划解决最长公共子串和最长公共子序列问题。

一、写在前面

当自己在网上搜什么是动态规划时，许许多多晦涩难懂的专业术语映入眼帘，令人望而生畏。然而动态规划遵循着一套固定的流程：递归的暴力解法->带备忘录的递归解法->非递归的动态规划解法。那么什么是动态规划呢？针对一个问题，我们把这个问题拆分成一个个子问题，然后将每个子问题的最优解记录下来(即”备忘录”)，相邻子问题之间层层递进，再根据子问题答案进行反推，最终得出原问题的最优解，这便是动态规划。简单一句话就是，拆分子问题，记住过往，减少重复计算。

二、最长公共子串

1.题目描述

给出两个字符串a和b的最长连续公共子串的长度。例如“abcbcde”和“bbcbce”的最长连续公共子串是“bcbc”，长度为4。

2.思路解析

假设字符串a和b的长度分别是m和n，绘制一张m×n的二维表格table[m][n]。取字符串a和b的字符前缀a’和b’，表格位置i，j上的数字含义是: 字符串a’和b’的且以它们尾巴字符结尾的最长公共子串的长度。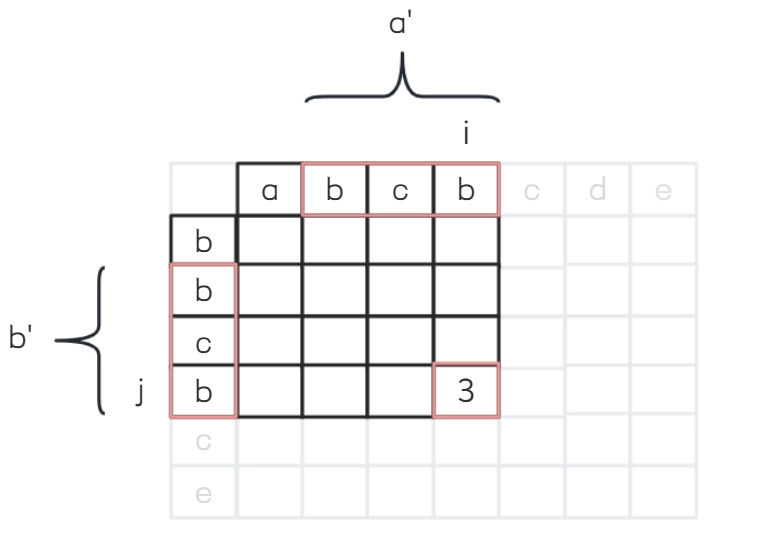

假设已经知道i-1和j-1处的数值，考虑i，j的数值：

• 如果新的a[i]和b[j]相等，则最长公共子串得到扩展，因此数值+1。
• 否则以两个字符为尾巴的最长公共子串不复存在，因此数值清零。
  下图中左右示例对应上述两种情况：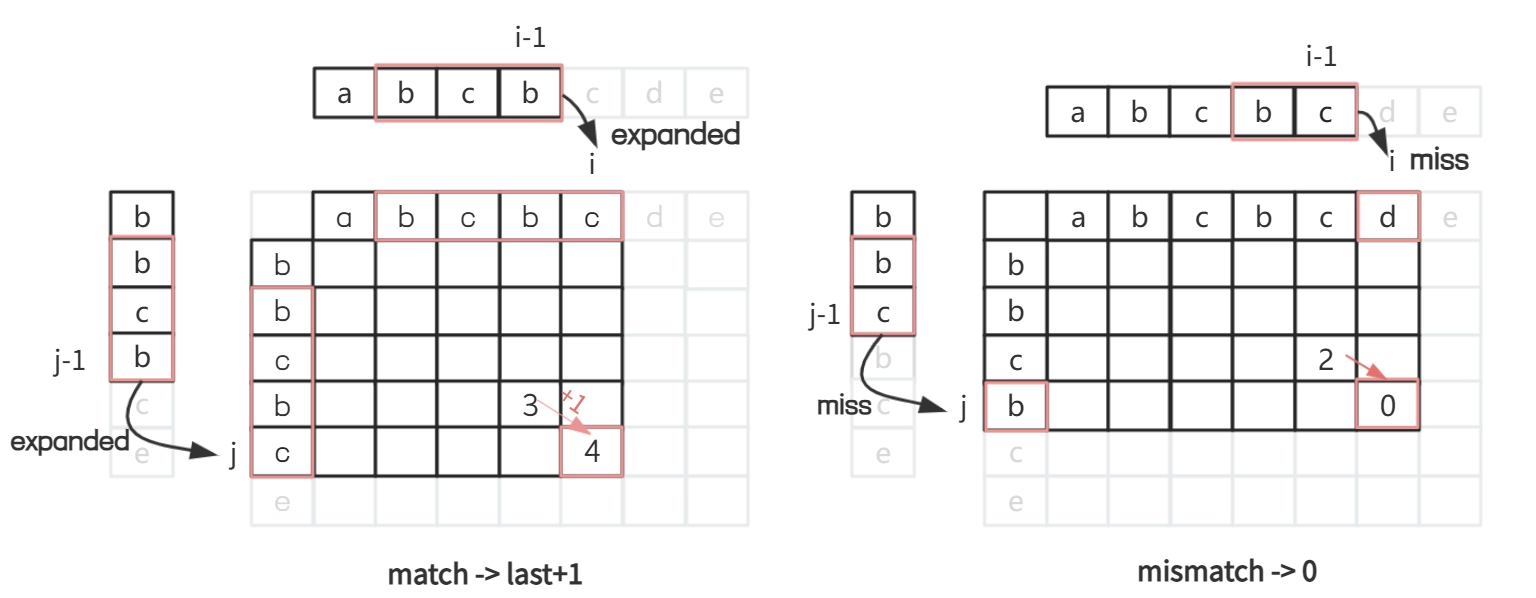
  
  于是得到填表规律：
• 如果当前格子对应的两个字符不同，则写0。
• 否则采用斜上方的格子的数值+1
  
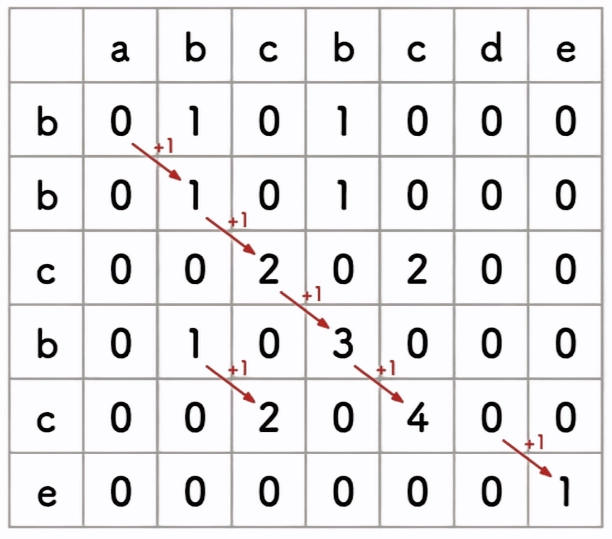
  用代码描述这个填表规则：
• 若a[i]!=b[j]，则填写table[i][j]=0
• 否则，填写table[i][j]=table[i-1][j-1]+1
  表格中的最大值即为最长公共子串的长度，时间复杂度为O(m*n)。

3.代码实现

// 返回字符串 a 和 b 的最长公共子串的长度
// 例如 "abcdbcdef" 和 "bbcbbcdee" 的公共字符串是 "bcde" 长度是 4
int LongestCommonSubstring(char *a, int a_length, char *b, int b_length) {
    int table[a_length][b_length];
    int max = 0;

    for (int i = 0; i < a_length; i++) {
        for (int j = 0; j < b_length; j++) {
            if (a[i] == b[j]) {
                if (i >= 1 && j >= 1)
                    table[i][j] = table[i - 1][j - 1] + 1;
                else
                    table[i][j] = 1;
            } else {
                table[i][j] = 0;
            }

            if (table[i][j] > max) {
                max = table[i][j];
            }
        }
    }

    return max;
}

三、最长公共子序列

1.题目描述

给出两个字符串a和b的最长公共子序列的长度。其和公共子串不同的是，公共子序列不要求连续。最长公共子序列是非常经典的动态规划问题，简称LCS问题。例如“abcbcde”和“acabdef”的最长公共子序列是“acbde”，长度为5。LeetCodet题目-最长公共子序列

2.思路解析

如果两个字符串的尾位置分别是i和j，假设它们的最长公共子序列的长度是函数f(i, j):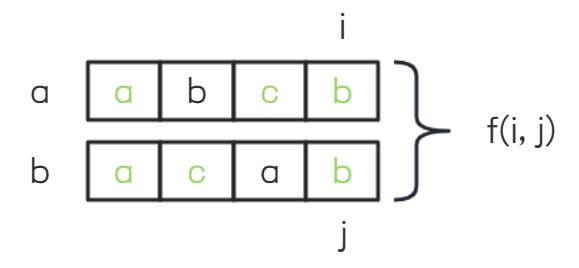
考虑函数的递推关系：

• 如果两个字符串的尾字符相同，易知f(i, j)=f(i-1, j-1)+1:
• 如果尾字符不同，上述递推关系则不成立:
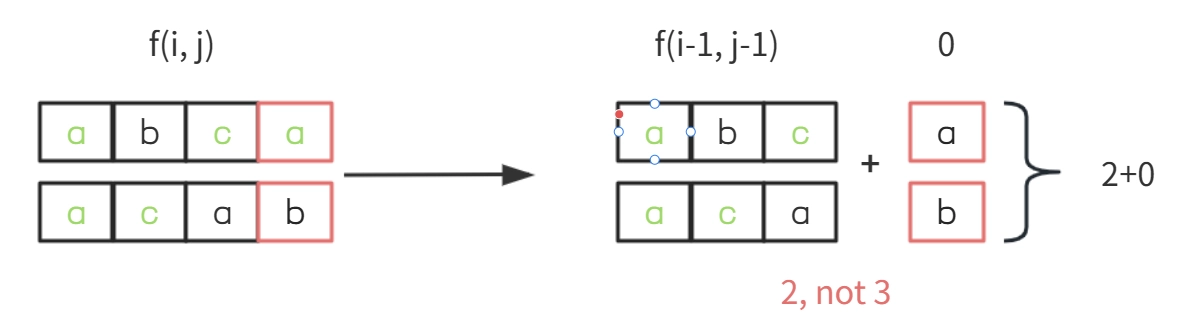
  原因在于，虽然尾字符不同，但一个字符串的尾字符可能和另一个字符串的前面的某个字符相同，导致最长公共子序列得到扩展。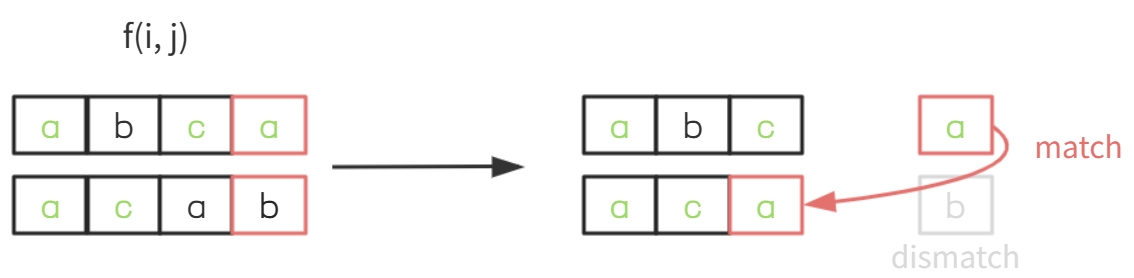
  注意，上图的关系可以进一步表达为：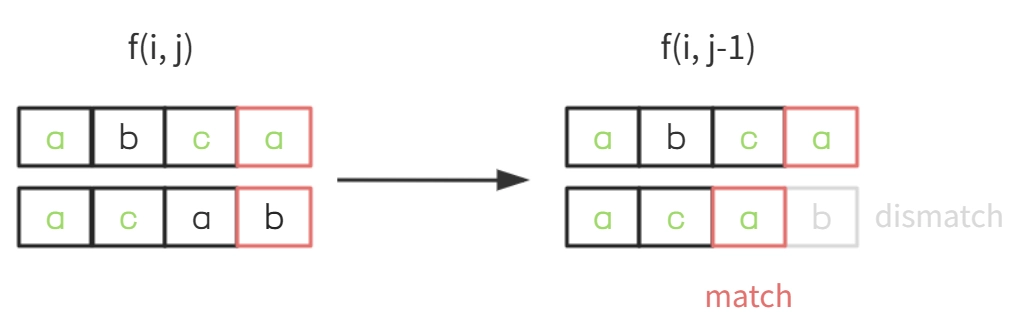
  考虑其一般性，取f(i-1, j)和f(i, j-1)的最大值: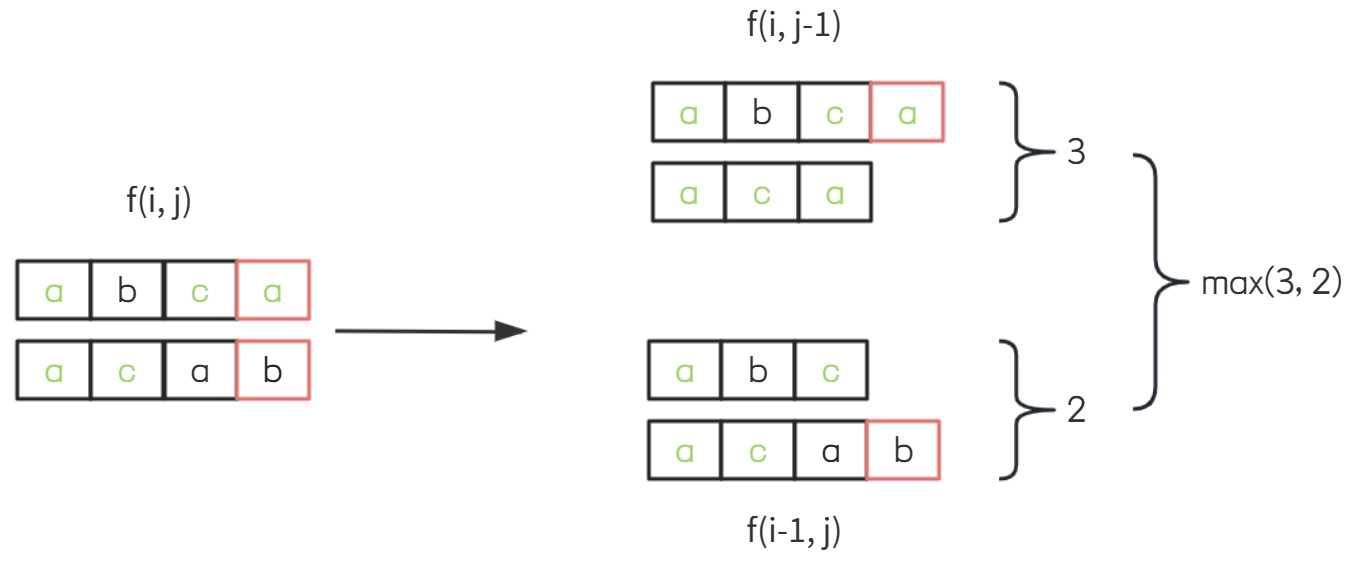
  假设字符串a和b的长度分别是m和n，绘制一张m×n的二维表格table[m][n]。取字符串a和b的前缀字符串“a’”和“b’”，表格位置i，j上的数字含义为f(i，j)即字符串a’和b’的最长公共子序列的长度。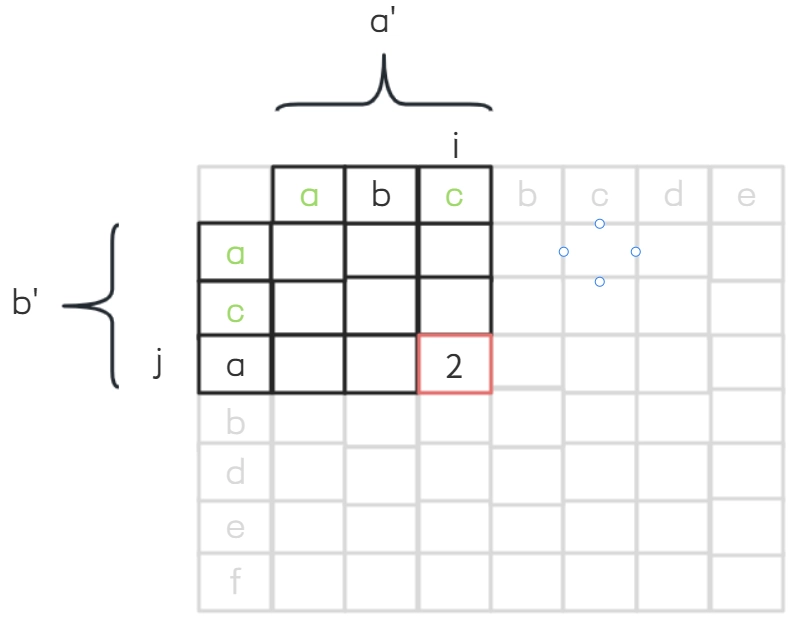
  利用已分析的递推关系，表格填写规则如下：
• 如果字符a[i]和b[j]相同，则最长公共子序列得到扩展，数值+1
• 否则，采用左边的和上面的方格中的数值的最大值
  
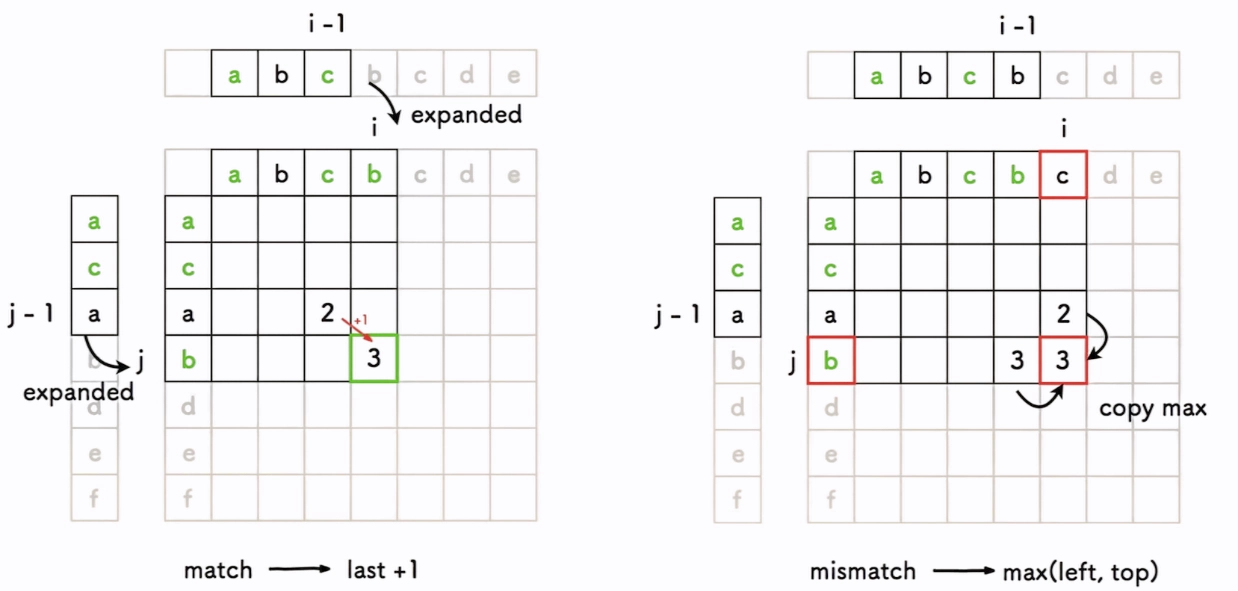
  按照上述规律，字符串“abcbcde”和“acabdef”的填表过程如下：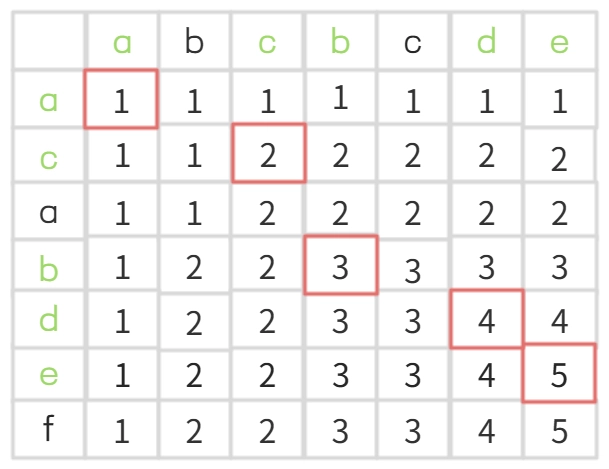
  上述规则映射至代码为：
• 若a[i]==b[j]，则填写table[i][j]=table[i-1][j-1]+1
• 否则填写table[i][j]=max(table[i-1][j], table[i][j-1])
  表格中最大值即为最长公共子序列的长度，时间复杂度为O(m*n)。

3.代码实现

#define MAX(a, b) (a) > (b) ? (a) : (b)

// 返回两个字符串 a 和 b 的最长公共子序列的长度
// 例如 "abcbcde" 和 "acabdef" 的最长公共子序列是 "acbde" ，长度为 5
int LongestCommonSubsequence(char *a, int a_length, char *b, int b_length) {
    int table[a_length][b_length];
    int max = 0;

    for (int i = 0; i < a_length; i++) {
        for (int j = 0; j < b_length; j++) {
            if (a[i] == b[j]) {
                if (i >= 1 && j >= 1)
                    table[i][j] = table[i - 1][j - 1] + 1;
                else
                    table[i][j] = 1;
            } else {
                if (i >= 1 && j >= 1)
                    table[i][j] = MAX(table[i - 1][j], table[i][j - 1]);
                else if (i <= 0 && j >= 1)
                    table[i][j] = table[i][j - 1];
                else if (i >= 1 && j <= 0)
                    table[i][j] = table[i - 1][j];
                else
                    table[i][j] = 0;
            }

            if (max < table[i][j]) max = table[i][j];
        }
    }
    return max;
}